线性回归

线性回归是解决回归问题最基本的一个方法。其实质就是找到一条直线能尽可能多的使已知的离散值分布在其周围（二维坐标系中）

就像这样：

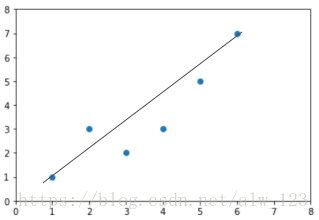
或者是在三维坐标中，找到一个面来逼近

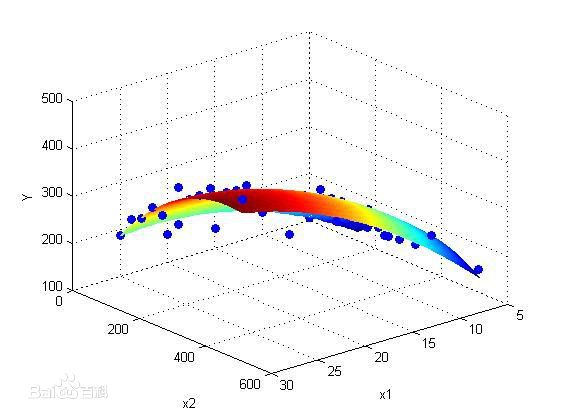
在这里我们只讨论最简单的单变量线性回归

单变量线性回归

单变量线性回归问题只含有一个特征（输入变量），因此可以把目标直线表达式写为：

h(x) = y = wx + b

其中， x代表特征/输入变量，h代表目标变量/输出变量

我们需要有一个包含许多对(x, y)的训练集，之后把它喂给我们的学习算法，学习算法输出一个函数，通常表示为小写h表示，代表hypothesis(假设)，表示一个函数

因此h根据输入的x值来得出y值，y值就是我们想要根据x知道的答案。因此，h是一个从y到x的函数映射。

代价函数

又称为“损失函数”

在前面的函数h中，我们选择的参数决定了我们得到的直线相对于我们的训练集的准确程度。

模型所预测的值与训练集中实际值之间的差距（下图中蓝线所指）就是建模误差（modeling error）

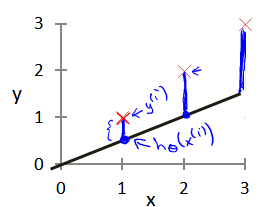
我们的目标便是选择出可以使得建模误差的平方和能够最小的模型参数。 即使得代价函数最小

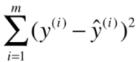
这个代价函数可以根据最小二乘法得到

我们绘制一个等高线图，三个坐标分别w (图中theta0)、h (图中theta1)和代价函数 (图中J(theta0, theta1))

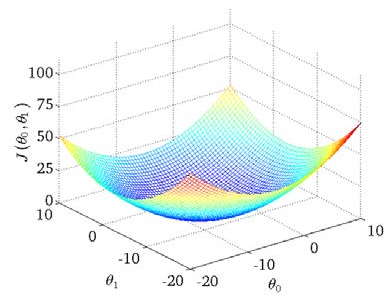
代价函数也被称作平方误差函数，有时也被称为平方误差代价函数。我们之所以要求出误差的平方和，是因为误差平方代价函数，对于大多数问题，特别是回归问题，都是一个合理的选择。还有其他的代价函数也能很好地发挥作用，但是平方误差代价函数可能是解决回归问题最常用的手段了。

参考资料： 吴恩达《机器学习》课程笔记