多变量梯度下降
与单变量线性回归类似,在多变量线性回归中,我们也构建一个代价函数,则这个代价函数是所有建模误差的平方和,即:
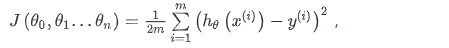
其中:
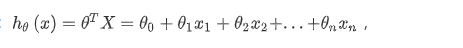
我们的目标和单变量线性回归问题中一样,是要找出使得代价函数最小的一系列参数。 多变量线性回归的批量梯度下降算法为:

我们开始随机选择一系列的参数值,计算所有的预测结果后,再给所有的参数一个新的值,如此循环直到收敛。
Python 代码示例:

def computeCost(X, y, theta):
inner = np.power(((X * theta.T) - y), 2)
return np.sum(inner) / (2 * len(X))
梯度下降法实践1-特征缩放
在我们面对多维特征问题的时候,我们要保证这些特征都具有相近的尺度,这将帮助梯度下降算法更快地收敛
以房价问题为例,假设我们使用两个特征,房屋的尺寸和房间的数量,尺寸的值为 0-2000平方英尺,而房间数量的值则是0-5,以两个参数分别为横纵坐标,绘制代价函数的等高线图能,看出图像会显得很扁,梯度下降算法需要非常多次的迭代才能收敛。
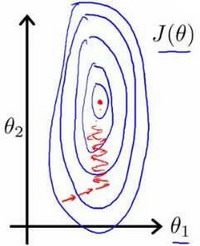
解决的方法是尝试将所有特征的尺度都尽量缩放到-1到1之间。如图:
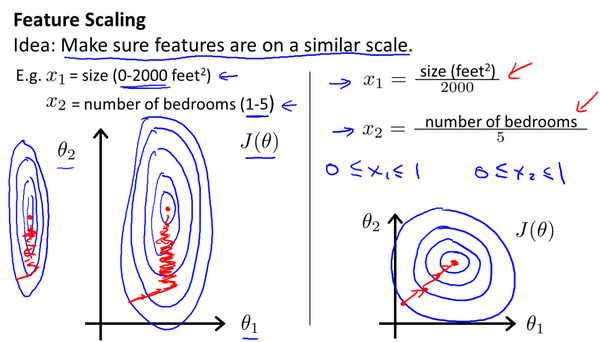
最简单的方法是令:x_n = (x_n - miu_n) / s_n ,其中miu_n是平均值,s_n是标准差
梯度下降法实践2—学习率
梯度下降算法收敛所需要的迭代次数根据模型的不同而不同,我们不能提前预知,我们可以绘制迭代次数和代价函数的图表来观测算法在何时趋于收敛。
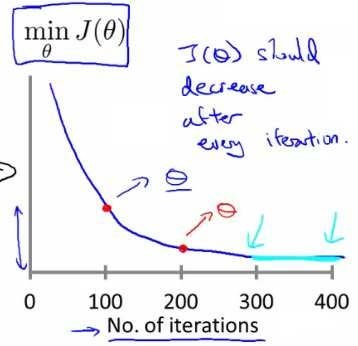
也有一些自动测试是否收敛的方法,例如将代价函数的变化值与某个阀值(例如0.001)进行比较,但通常看上面这样的图表更好
梯度下降算法的每次迭代受到学习率的影响,如果学习率过小,则达到收敛所需的迭代次数会非常高;如果学习率过大,每次迭代可能不会减小代价函数,可能会越过局部最小值导致无法收敛。
通常可以考虑尝试这些学习率:
alpha = 0.01, 0.03, 0.1, 0.3, 1, 3, 10
特征和多项式回归
对于房价预测问题

其中,x1 = frontage(临街宽度),x2 = depth(纵向深度),x = frontage * depth = area,则:h(x) = theta0 + theta1*x1 + theta2*x2^2
线性回归并不适用于所有数据,有时我们需要曲线来适应我们的数据,比如一个二次方模型:h(x) = theta0 + theta1*x1 + theta2*x2^2 或者三次方模型:h(x) = theta0 + theta1*x1 + theta2*x2^2 + theta3*x3^3
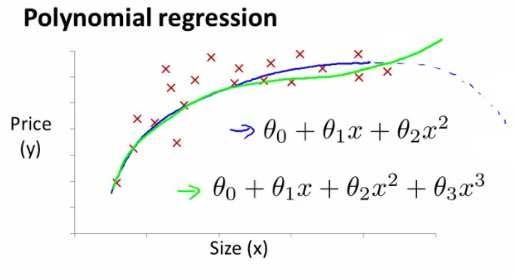
通常我们需要先观察数据然后再决定准备尝试怎样的模型。 另外,我们可以令:x2 = x2^2, x3 = x3^3,从而将模型转化为线性回归模型。
根据函数图形特性,我们还可以使:

注:如果我们采用多项式回归模型,在运行梯度下降算法前,特征缩放非常有必要。
正规方程
对于某些线性回归问题,正规方程方法是更好的解决方案。如
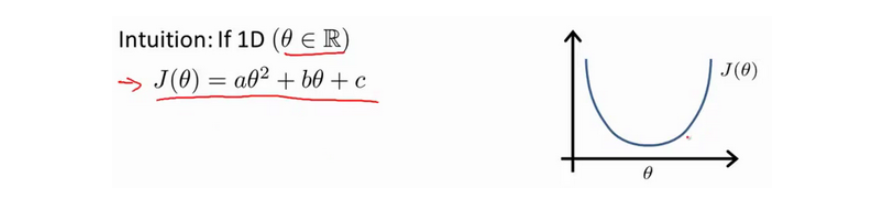
正规方程是通过求解下面的方程来找出使得代价函数最小的参数的:
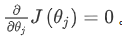
即对J(theta)进行求导。
假设我们的训练集特征矩阵为X(包含了x0=1),并且我们的训练集结果为向量y,则利用正规方程解出向量
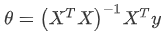
对于某些不可逆的矩阵(通常是因为特征之间不独立,如同时包含英尺为单位的尺寸和米为单位的尺寸两个特征,也有可能是特征数量大于训练集的数量),则无法使用正规方程方法

以下表数据为例:
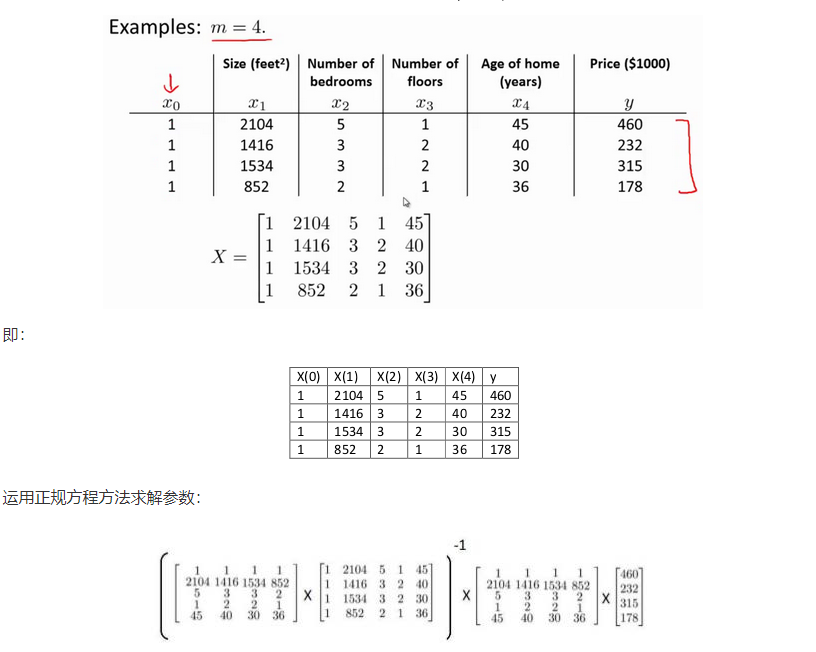
梯度下降与正规方程的比较:
| 梯度下降 | 正规方程 |
|---|---|
需要选择学习率Alpha |
不需要 |
| 需要多次迭代 | 一次运算得出 |
当特征数量n大时也能较好适用 |
需要计算A的逆如果特征数量n较大则运算代价大,因为矩阵逆的计算时间复杂度为O(n^3),通常来说当n小于10000时还是可以接受的 |
| 适用于各种类型的模型 | 只适用于线性模型,不适合逻辑回归模型等其他模型 |
只要特征变量的数目并不大,正规方程是一个很好的计算参数theta的替代方法。具体地说,只要特征变量数量小于一万,通常使用正规方程法,而不使用梯度下降法。
对于那些更复杂的学习算法,我们将不得不仍然使用梯度下降法。因此,梯度下降法是一个非常有用的算法,可以用在有大量特征变量的线性回归问题。
但对于这个特定的线性回归模型,标准方程法是一个比梯度下降法更快的替代算法。所以,根据具体的问题,以及你的特征变量的数量,这两种算法都是值得学习的。
正规方程的Python实现:
import numpy as np
def normalEqn(X, y):
theta = np.linalg.inv(X.T@X)@X.T@y
#X.T@X等价于X.T.dot(X)
return theta