梯度下降

梯度下降是一个用来求函数最小值的算法，在这里我们将使用梯度下降算法来求出代价函数（损失函数）J(w1, w2)的最小值

假设我们有时间和计算资源来计算权重值w1的所有可能值的损失。对于回归问题，所产生的损失与w1的图形始终是碗状图，如下所示：

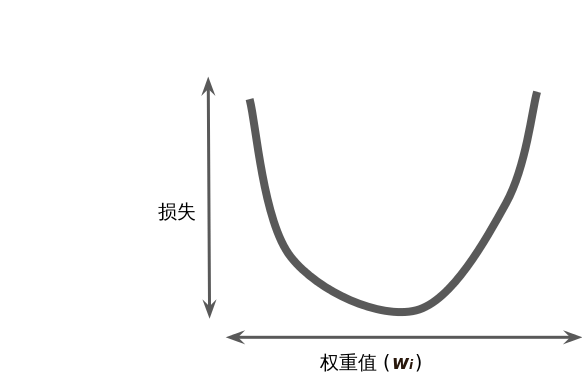
图中的最低点，即斜率正好为 0的位置。这个最小值就是损失函数收敛之处。

过程

开始时我们为(w1, w2)选择一个起始值（起点）。然而起点并不重要；因此很多算法就直接将它们设为0或随机选择一个值。

通过这个参数组合计算代价函数，然后我们寻找下一个能让代价函数值下降最多的参数组合。

在这里使用梯度下降法算法计算损失曲线在起点处的梯度。梯度是偏导数的矢量；它可以让我们了解哪个方向距离目标“更近”或“更远”

梯度始终指向损失函数中增长最为迅猛的方向。梯度下降法算法会沿着负梯度的方向走一步，以便尽快降低损失。

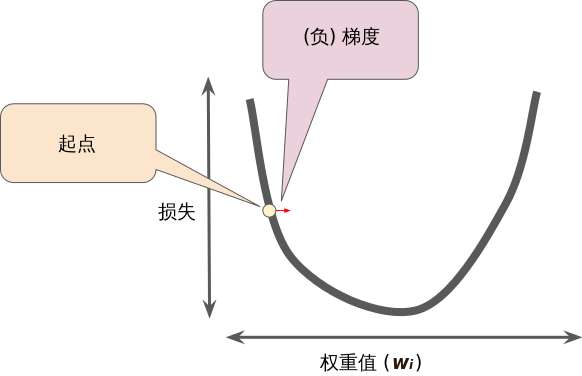
为了确定损失函数曲线上的下一个点，梯度下降法算法会将梯度大小的一部分与起点相加：

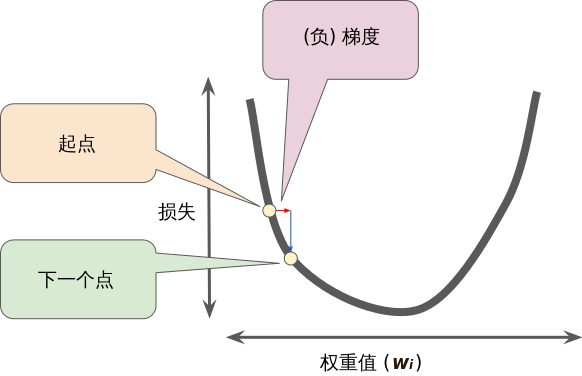
然后，梯度下降法会重复此过程，逐渐接近最低点。

局部最小值

想象一下你正站立在山的这一点上，站立在你想象的公园这座红色山上，在梯度下降算法中，我们要做的就是旋转360度，看看我们的周围，并问自己要在某个方向上，用小碎步尽快下山。

这些小碎步需要朝什么方向？如果我们站在山坡上的这一点，你看一下周围，你会发现最佳的下山方向，你再看看周围，然后再一次想想，我应该从什么方向迈着小碎步下山？然后你按照自己的判断又迈出一步，重复上面的步骤，从这个新的点，你环顾四周，并决定从什么方向将会最快下山，然后又迈进了一小步，并依此类推，直到你接近局部最低点的位置。

我们持续这么做直到我们得到一个局部最小值（local minimum），然而因为我们并没有尝试完所有的参数组合，所以不能确定我们得到的局部最小值是否便是全局最小值（global minimum），如果选择不同的初始参数组合，可能会找到不同的局部最小值。

这个问题在以前的机器学习中可能会遇到，因为机器学习中的特征比较少，所以导致很可能陷入到一个局部最优解中出不来 但是到了深度学习，动辄百万甚至上亿的特征，出现这种情况的概率几乎为0，所以我们可以不用考虑这个问题。

批量梯度下降

批量梯度下降法是最原始的形式，它是指在每一次迭代时使用所有样本来进行梯度的更新

公式为：

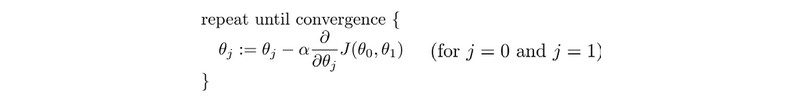
其中alpha是学习率（learning rate），它决定了我们沿着能让代价函数下降程度最大的方向向下迈出的步子有多大，在批量梯度下降中，我们每一次都同时让所有的参数减去学习速率乘以代价函数的导数。

在梯度下降算法中，还有一个更微妙的问题，梯度下降中，我们要更新theta0和theta1，当j = 0和j = 1时，会产生更新，所以你将更新J(theta0)和J(theta1)。

实现梯度下降算法的微妙之处是，在这个表达式中，如果你要更新这个等式，你需要同时更新theta0和theta1，我的意思是在这个等式中，我们要这样更新：

theta0:=theta0，并更新theta1:=theta1

实现方法是：你应该计算公式右边的部分，通过那一部分计算出theta0和theta1的值，然后同时更新theta0和theta1。

学习率 Alpha

让我们来看看如果太小或太大会出现什么情况：

• 如果太小了，即我的学习速率太小，结果就是只能这样像小宝宝一样一点点地挪动，去努力接近最低点，这样就需要很多步才能到达最低点，所以如果太小的话，可能会很慢，因为它会一点点挪动，它会需要很多步才能到达全局最低点。

• 如果太大，那么梯度下降法可能会越过最低点，甚至可能无法收敛，下一次迭代又移动了一大步，越过一次，又越过一次，一次次越过最低点，直到你发现实际上离最低点越来越远，所以，如果太大，它会导致无法收敛，甚至发散。

假设你将theta1初始化在局部最低点，在这儿，它已经在一个局部的最优处或局部最低点。结果是局部最优点的导数将等于零，因为它是那条切线的斜率。这意味着你已经在局部最优点，它使得theta1不再改变，也就是新的theta1等于原来的theta1，因此，如果你的参数已经处于局部最低点，那么梯度下降法更新其实什么都没做，它不会改变参数的值。这也解释了为什么即使学习速率alpha保持不变时，梯度下降也可以收敛到局部最低点。

在梯度下降法中，当我们接近局部最低点时，梯度下降法会自动采取更小的幅度，这是因为当我们接近局部最低点时，很显然在局部最低时导数等于零，所以当我们接近局部最低时，导数值会自动变得越来越小，所以梯度下降将自动采取较小的幅度，这就是梯度下降的做法。所以实际上没有必要再另外减小。

这就是梯度下降算法，你可以用它来最小化任何代价函数，不只是线性回归中的代价函数。