当开发学习算法时，往往几个简单的图，可以让你更好地理解算法的内容，并且可以完整地检查下算法是否正常运行，是否达到了算法的目的。

二维绘图

我们先来快速生成一些数据用来绘图。

>> t = [0:0.01:0.98];
>> y1 = sin(2*pi*4*t);

如果我们想要绘制正弦函数，只需输入plot(t, y1)，如图

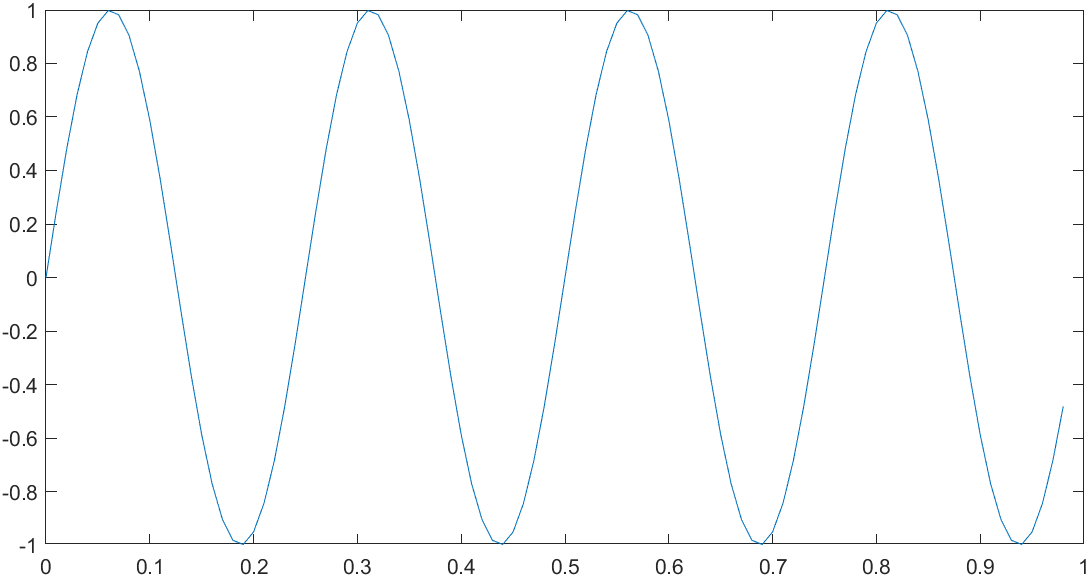
横轴是变量t，纵轴是y1，也就是我们刚刚所输出的正弦函数。

让我们设置y2

>> y2 = cos(2*pi*4*t);
>> plot(t, y2)

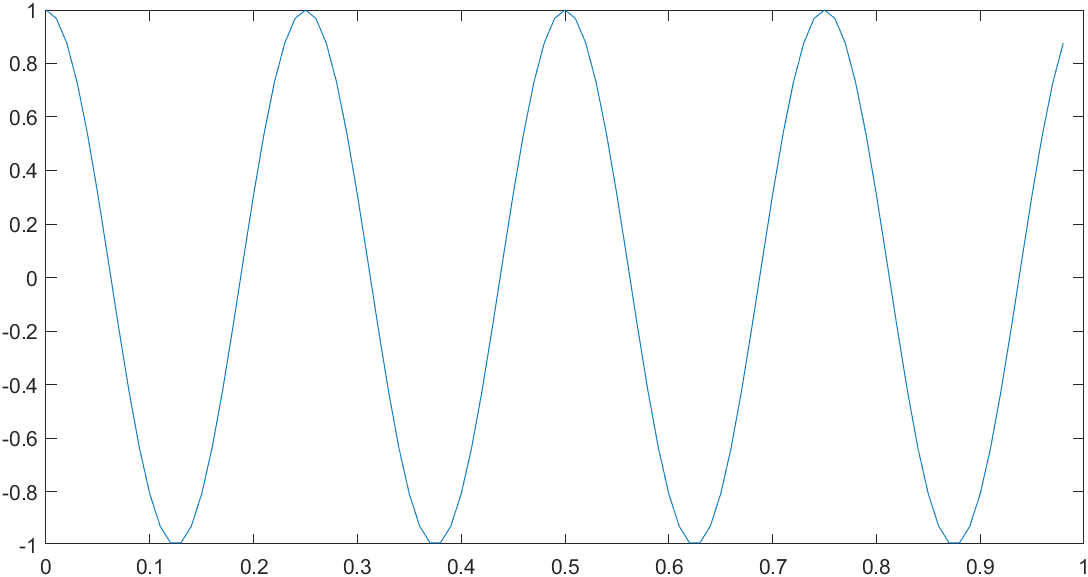
如果要同时表示正弦和余弦曲线。

我们要做的就是，输入：plot(t, y1)，得到正弦函数，之后使用函数hold on，它的功能是将新的图像绘制在旧的之上

再输入：plot(t, y2)，MATLAB会自动用不同颜色绘制新的曲线，我们也可以指定颜色，比如plot(t, y2, 'r')，r表示使用红色绘制y2

‘r’ 为线条设定。每个设定可包含表示线条颜色、样式和标记的字符。标记是在绘制的每个数据点上显示的符号，例如，+、o 或 * ；

例如，‘g:*’ 请求绘制使用 * 标记的绿色点线。‘r–‘请求红色虚线

还可以使用命令xlabel('time')标记X轴，输入ylabel('value')标记Y轴的值。

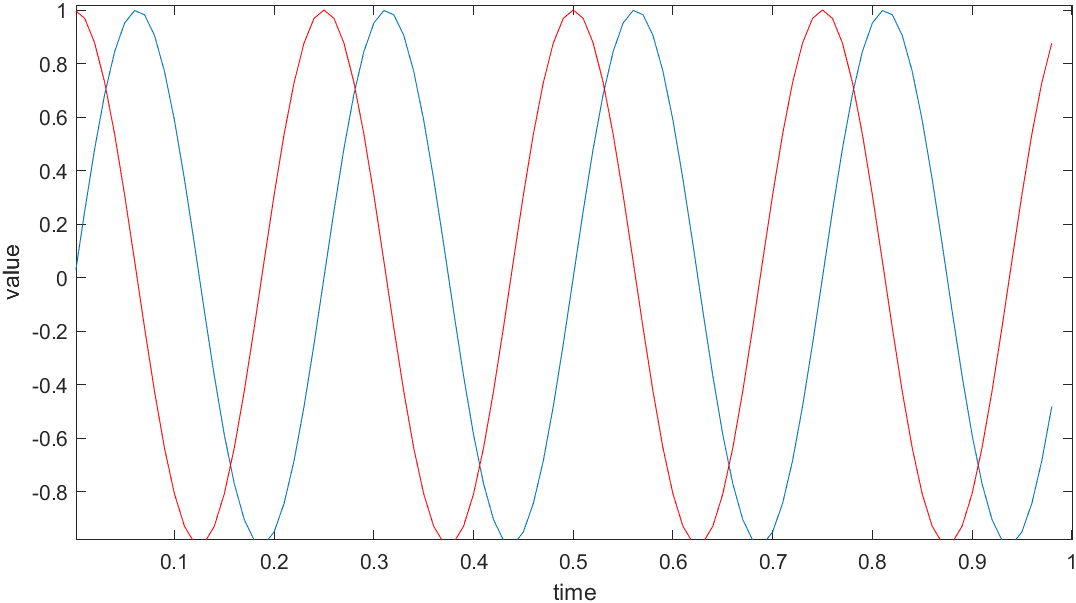
同时我们也可以标记这两条函数曲线，用命令 legend('sin','cos')将这个图例放在右上方，表示这两条曲线表示的内容。最后输入title('myplot')，在图像的顶部显示这幅图的标题。

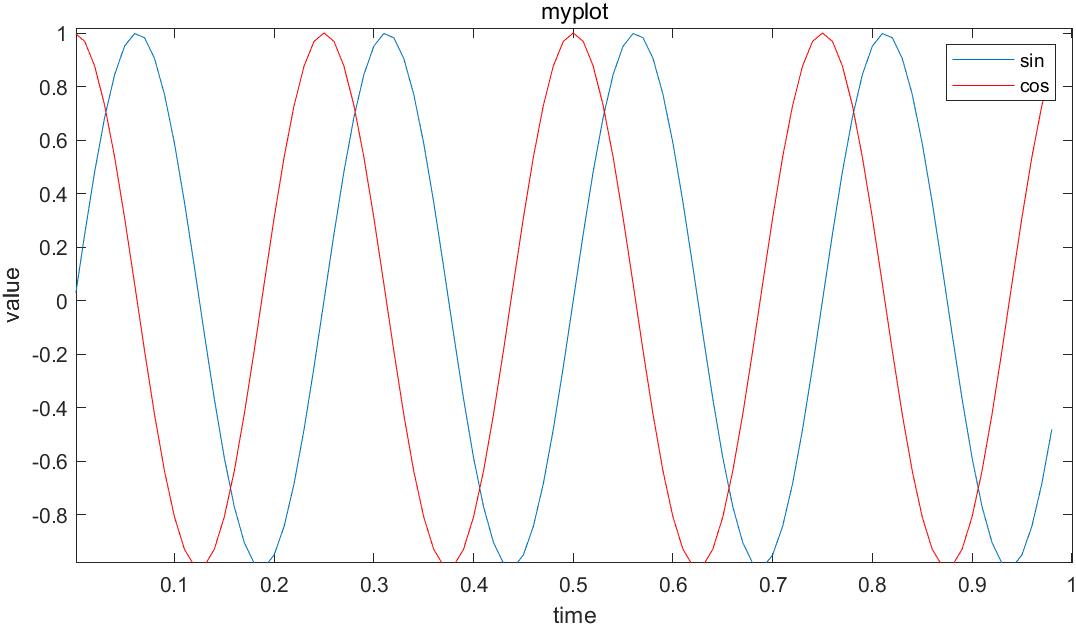
使用close命令可以关掉图像

可以为图像标号

• 使用figure(1); plot(t, y1);将显示第一张图，绘制了y1-t

• 使用figure(2); plot(t, y2);将显示第一张图，绘制了y2-t

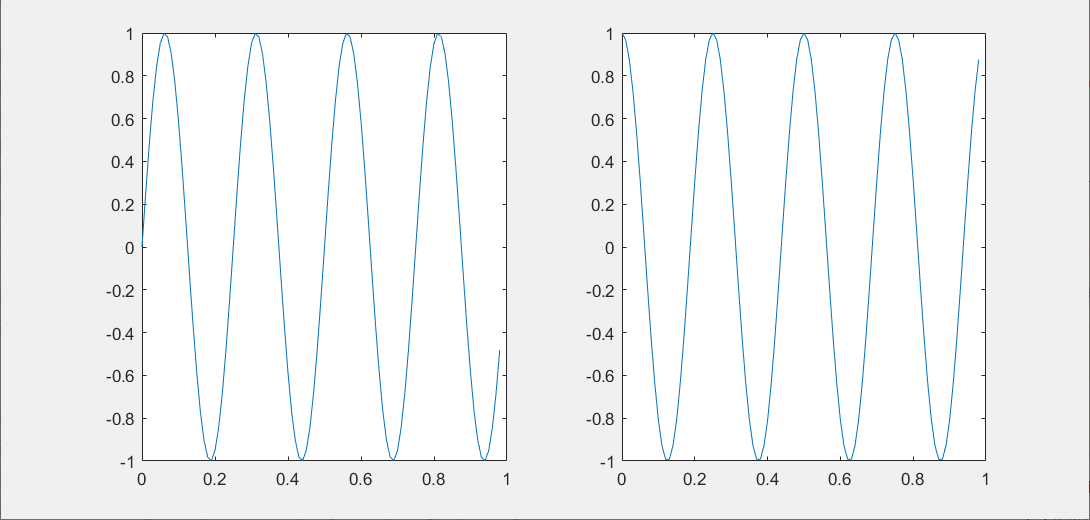
subplot命令，我们使用subplot(1,2,1)，它将图像分为一个1*2的格子，也就是前两个参数，然后它使用第一个格子，也就是最后一个参数1的意思。

之后键入plot(t, y1)，y1-t图显示在第一个格子；

使用subplot(1, 2, 2); plot(t, y2)，y2-t图显示在第二个格子

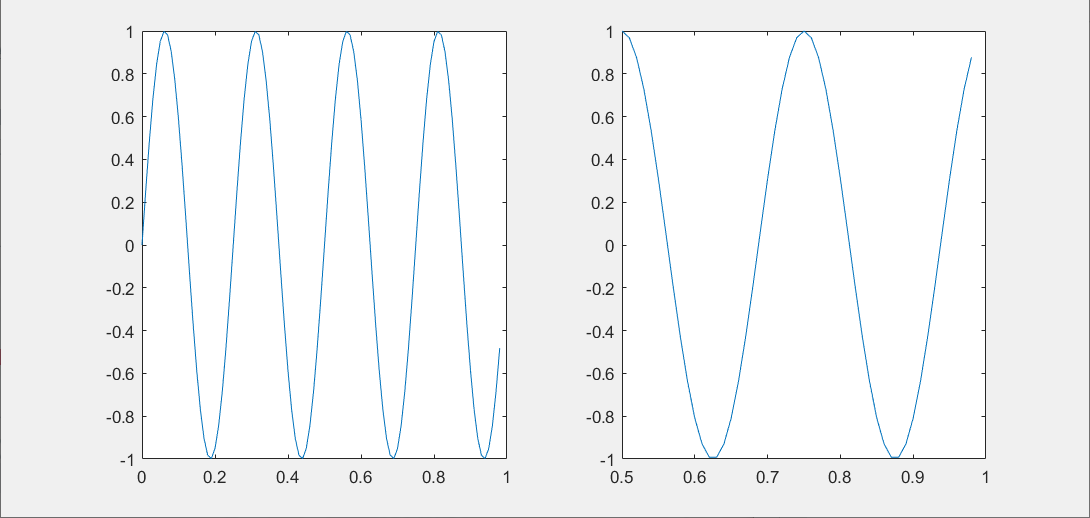
还有一个命令，可以改变轴的刻度，比如改成[0.5 1 -1 1]，输入命令：axis([0.5 1 -1 1])也就是设置了右边图的轴和轴的范围。具体而言，它将右图中的横轴的范围调整至0.5到1，竖轴的范围为-1到1。

clf命令可以清除当前的Figure

imagesc

首先我们设置A等于一个5×5的magic方阵：

>> A = magic(5)
A =
    17    24     1     8    15
    23     5     7    14    16
     4     6    13    20    22
    10    12    19    21     3
    11    18    25     2     9

可以通过imagesc(A)来可视化矩阵，它将会绘制一个5 * 5的矩阵，一个5 * 5的彩色格图，不同的颜色对应A矩阵中的不同值

还可以使用函数colorbar：使用一个更复杂的命令 imagesc(A),colorbar,colormap gray。这实际上是在同一时间运行三个命令：运行imagesc，然后运行colorbar，然后运行colormap gray。

它生成了一个颜色图像，一个灰度分布图，并在右边也加入一个颜色条。所以这个颜色条显示不同深浅的颜色所对应的值。

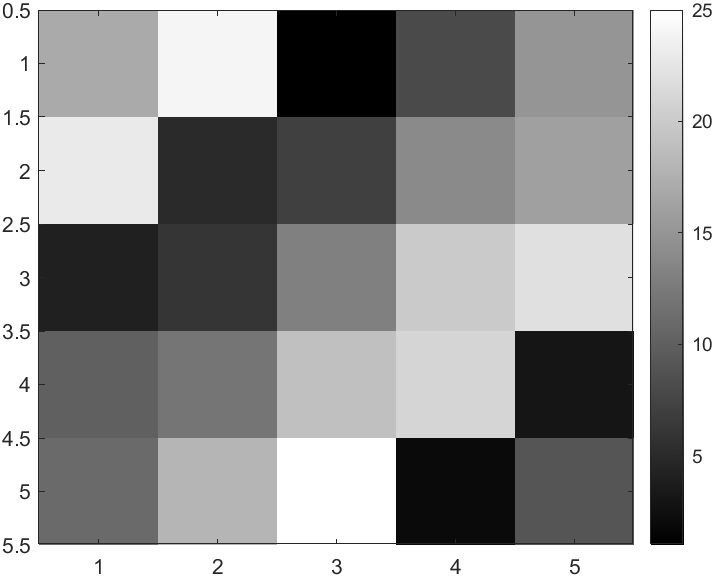
可以看到在不同的方格，它对应于一个不同的灰度。

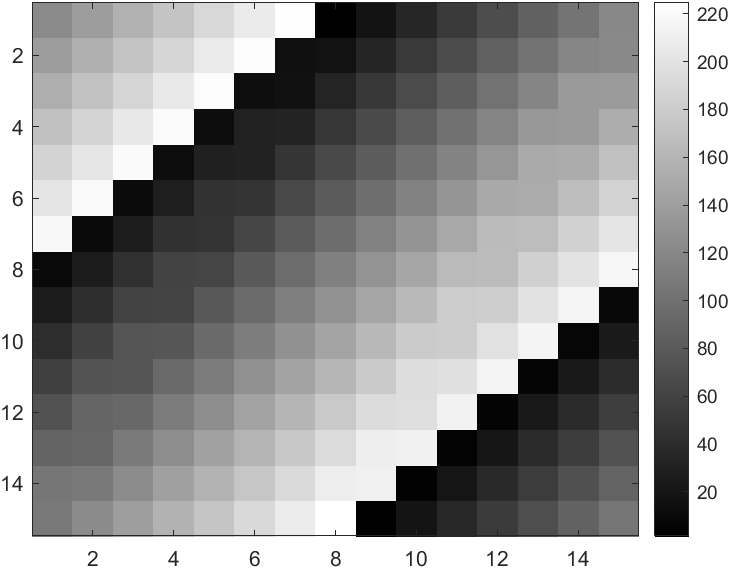
输入imagesc(magic(15)),colorbar,colormap gray，获得一幅15*15的magic方阵值图

三维绘图

三维图通常显示一个由带两个变量的函数（即 z = f (x,y)）定义的曲面图。

要计算 z，首先使用 meshgrid 在此函数的域中创建一组 (x,y) 点。

>> [X,Y] = meshgrid(-2:.2:2); 
>> Z = X .* exp(-X.^2 - Y.^2);

meshgrid函数生成的X，Y是大小相等的矩阵

然后创建曲面图

surf(X, Y, Z)

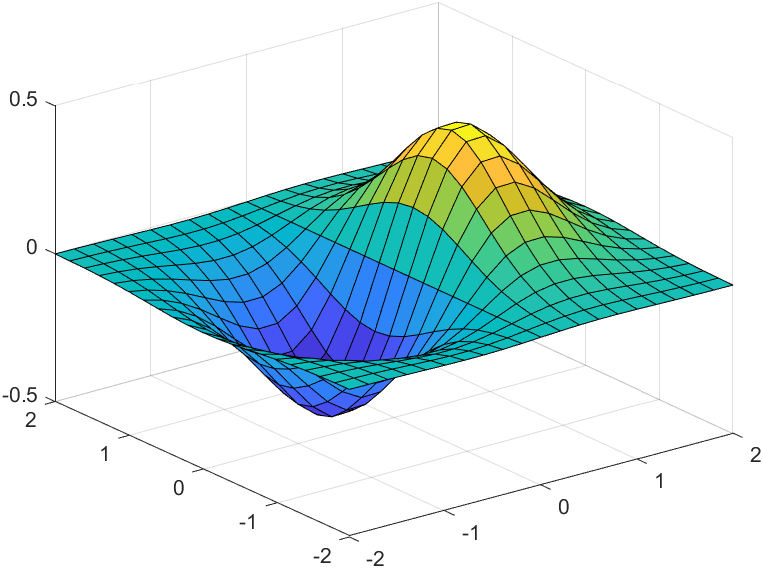
surf 函数及其伴随函数 mesh 以三维形式显示曲面图。surf 使用颜色显示曲面图的连接线和面。mesh 生成仅以颜色标记连接定义点的线条的线框曲面图。