Autograd 自动求导机制

PyTorch 中所有神经网络的核心是 autograd 包。

autograd 包为张量上的所有操作提供了自动求导。它是一个在运行时定义的框架，可以通过代码的运行来决定反向传播的过程，并且每次迭代可以是不同的。

通过一些示例来了解

Tensor 张量

torch.tensor是这个包的核心类。

• 设置.requires_grad为True，会追踪所有对于该张量的操作。计算完成后调用.backward()，可以自动计算所有的梯度，并自动累计到.grad属性中

事实上即使.requires_grad为True并不意味着.grad一定不为None

• 可以调用.detach()将该张量与计算历史记录分离，并禁止跟踪它将来的计算记录

• 为防止跟踪历史记录（和使用内存），可以将代码块包装在with torch.no_grad(): 中。这在评估模型时特别有用，因为模型可能具有requires_grad = True的可训练参数，但是我们不需要梯度计算。

Function类

Tensor 和 Function 互相连接并生成一个非循环图，它表示和存储了完整的计算历史。

每个张量都有一个.grad_fn属性，对张量进行操作后，grad_fn会引用一个创建了这个Tensor类的Function对象（除非这个张量是用户手动创建的，此时，这个张量的 grad_fn 是 None）

leaf Tensors 叶张量

Tensor中有一属性is_leaf，当它为True有两种情况：

1. 按照惯例，requires_grad = False 的 Tensor

2. requires_grad = True 且由用户创建的 Tensor。这意味着它们不是操作的结果且grad_fn = None

只有leaf Tensors叶张量在反向传播时才会将本身的grad传入backward()的运算中。要想得到non-leaf Tensors非叶张量在反向传播时的grad，可以使用retain_grad()

如果需要计算导数，可以在Tensor上调用.backward()：若Tensor是一个标量（即包含一个元素数据）则不需要为backward()指定任何参数， 但是如果它有更多的元素，需要指定一个gradient 参数来匹配张量的形状。

x = torch.ones(2, 2, requires_grad=True)
print(x) 
# Output:
# tensor([[1., 1.],
#        [1., 1.]], requires_grad=True)
y = x + 2
print(y)
# Output:
# tensor([[3., 3.],
#        [3., 3.]], grad_fn=<AddBackward0>)

此时，y已经被计算出来，grad_fn已经自动生成了

>>> print(y.grad_fn)
<AddBackward0 object at 0x0000013D6C2AB848>

对y进行操作

z = y * y * 3
out = z.mean()
print(z, out)
# Output:
# tensor([[27., 27.],
#        [27., 27.]], grad_fn=<MulBackward0>) # tensor(27., grad_fn=<MeanBackward0>)

.requires_grad_( ... ) 可以改变现有张量的 requires_grad属性。 如果没有指定的话，默认输入的flag是 False

Gradients 梯度

现在开始反向传播

因为out是一个标量，因此不需要为backward()指定任何参数：

out.backward()
print(x.grad)
# Output:
# tensor([[4.5000, 4.5000],
#        [4.5000, 4.5000]])

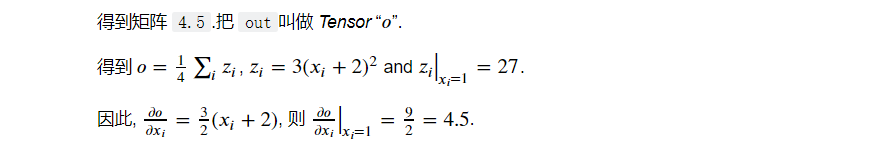
现在让我们来看一个vector-Jacobian product的例子

x = torch.randn(3, requires_grad=True)
y = x * 2
while y.data.norm() < 1000:
    y = y * 2
print(y) 
# Output:
# tensor([ 293.4463,   50.6356, 1031.2501], grad_fn=<MulBackward0>)

此处y.data.norm()指y的范数，即(y_1^2 + … + y_n^2)^(1/2)

在这个情形中，y不再是个标量。torch.autograd无法直接计算出完整的雅可比行列，但是如果我们只想要vector-Jacobian product，只需将向量作为参数传入backward：

v = torch.tensor([0.1, 1.0, 0.0001], dtype=torch.float)
y.backward(v)
print(x.grad)
# Output:
# tensor([5.1200e+01, 5.1200e+02, 5.1200e-02])

如果.requires_grad=True但是你又不希望进行autograd的计算， 那么可以将变量包裹在 with torch.no_grad()中:

print(x.requires_grad) # True
print((x ** 2).requires_grad) # True

with torch.no_grad():
	print((x ** 2).requires_grad) # False

Autograd 过程

推导

grad_fn中有一属性next_functions，例如

x = torch.rand(5, 5, requires_grad=True)
y = torch.rand(5, 5, requires_grad=True)
z = x**2 + y**3
print(z.grad_fn) # <AddBackward0 at 0x1426dca72c8>
print(z.grad_fn.next_functions) 
# ((<PowBackward0 at 0x1426dc923c8>, 0), (<PowBackward0 at 0x1426dc92b48>, 0))

此处的next_functions是一个“tuple of tuple of PowBackward0 and int”

内层第一个tuple就是x相关的操作记录，继续深入

xg = z.grad_fn.next_functions[0][0]
x_leaf = xg.next_functions[0][0]
print(type(x_leaf)) # AccumulateGrad

在Pytorch的反向图计算中，AccumulateGrad类型代表的就是叶子节点类型，也就是计算图的终止节点。

AccumulateGrad中有一个.variable指向叶子节点

x_leaf.variable

这个.variable的属性就是我们的生成的变量x

流程

1. 当我们执行z.backward()时。这个操作将调用z里面的grad_fn属性，执行求导操作。
2. 这个操作将遍历grad_fn的next_functions，然后分别取出里面的Function(AccumulateGrad)，执行求导操作。这部分是一个递归的过程直到最后类型为叶子节点。
3. 计算出结果以后，将结果保存到他们对应的variable 变量所引用的对象（x和y）的grad属性中
4. 求导结束。所有的叶节点的grad变量都得到了相应的更新

最终当我们执行完c.backward()之后，a和b里面的grad值就得到了更新。

拓展Autograd

如果需要自定义autograd扩展新的功能，就需要扩展Function类。因为Function使用autograd来计算结果和梯度，并对操作历史进行编码。

在Function类中最主要的方法就是forward()和backward()他们分别代表了前向传播和反向传播。

一个自定义的Function需要一下三个方法：

• __init__ (optional)：如果这个操作需要额外的参数则需要定义这个Function的构造函数，不需要的话可以忽略。

• forward()：执行前向传播的计算代码

• backward()：反向传播时梯度计算的代码。 参数的个数和forward返回值的个数一样，每个参数代表传回到此操作的梯度。